|
STXXL
1.4.1
|
|
STXXL
1.4.1
|
The development of STXXL has been started with sorting, because it is the fundamental tool for I/O-efficient processing of large data sets. Therefore, an efficient implementation of sorting largely defines the performance of an external memory software library as a whole. To achieve the best performance our implementation [26] uses parallel disks, has an optimal I/O volume 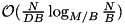 (that matches the lower bound), and guarantees almost perfect overlap between I/O and computation.
(that matches the lower bound), and guarantees almost perfect overlap between I/O and computation.
No previous implementation has all these properties, which are needed for a good practical sorting. LEDA-SM [25] and TPIE [7] concentrate on single disk implementations. For the overlapping of I/O and computation they rely on prefetching and caching provided by the operating system, which is suboptimal since the system knows little about the application's access pattern.
Barve and Vitter implemented a parallel disk algorithm [12] that can be viewed as the immediate ancestor of our algorithm. Innovations with respect to our sorting are: A different allocation strategy that enables better theoretical I/O bounds [34] [35]; a prefetching algorithm that optimizes the number of I/O steps and never evicts data previously fetched; overlapping of I/O and computation; a completely asynchronous implementation that reacts flexibly to fluctuations in disk speeds; and an implementation that sorts many GBytes and does not have to limit internal memory size artificially to obtain a nontrivial number of runs. Additionally, our implementation is not a prototype, it has a generic interface and is a part of the software library STXXL.
Algorithms in [49] [19] [20] have the theoretical advantage of being deterministic. However, they need three passes over data even for not too large inputs.
Prefetch buffers for disk load balancing and overlapping of I/O and computation have been intensively studied for external memory merge sort ([46] [18] [5] [34] [35] [37]). But we have not seen results that guarantee overlapping of I/O and computation during the parallel disk merging of arbitrary runs.
There are many good practical implementations of sorting (e.g. [43] [2] [44] [57]) that address parallel disks, overlapping of I/O and computation, and have a low internal overhead. However, we are not aware of fast implementations that give theoretical performance guarantees on achieving asymptotically optimal I/O. Most practical implementations use a form of striping that requires 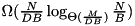 I/Os rather than the optimal
I/Os rather than the optimal 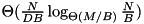 . This difference is usually considered insignificant for practical purposes. However, already on our experimental system we have to go somewhat below the block sizes that give the best performance if the input size is 128~GBytes. Another reduction of the block size by a factor of eight (we have eight disks) could increase the run time significantly. We are also not aware of high performance implementations that guarantee overlap of I/O and computation during merging for inputs such as the one described in Overlapping I/O and Merging.
. This difference is usually considered insignificant for practical purposes. However, already on our experimental system we have to go somewhat below the block sizes that give the best performance if the input size is 128~GBytes. Another reduction of the block size by a factor of eight (we have eight disks) could increase the run time significantly. We are also not aware of high performance implementations that guarantee overlap of I/O and computation during merging for inputs such as the one described in Overlapping I/O and Merging.
On the other hand, many of the practical merits of our implementation are at least comparable with the best current implementations: We are close to the peak performance of our system.
Perhaps the most widely used external memory sorting algorithm is k-way merge sort: During run formation, chunks of 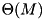 elements are read, sorted internally, and written back to the disk as sorted runs. The runs are then merged into larger runs until only a single run is left.
elements are read, sorted internally, and written back to the disk as sorted runs. The runs are then merged into larger runs until only a single run is left. 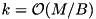 runs can be sorted in a single pass by keeping up to B of the smallest elements of each run in internal memory. Using randomization, prediction of the order in which blocks are accessed, a prefetch buffer of
runs can be sorted in a single pass by keeping up to B of the smallest elements of each run in internal memory. Using randomization, prediction of the order in which blocks are accessed, a prefetch buffer of 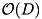 blocks, and an optimal prefetching strategy, it is possible to implement k-way merging using D disks in a load balanced way [34]. However, the rate at which new blocks are requested is more difficult to predict so that this algorithm does not guarantee overlapping of I/O and computation. In this section, we derive a parallel disk algorithm that compensates these fluctuations in the block request rate by a FIFO buffer of
blocks, and an optimal prefetching strategy, it is possible to implement k-way merging using D disks in a load balanced way [34]. However, the rate at which new blocks are requested is more difficult to predict so that this algorithm does not guarantee overlapping of I/O and computation. In this section, we derive a parallel disk algorithm that compensates these fluctuations in the block request rate by a FIFO buffer of 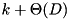 blocks.
blocks.
There are many ways to overlap I/O and run formation. We start with a very simple method that treats internal sorting as a black box and therefore can use the fastest available internal sorters. Two threads cooperate to build k runs of size 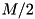 :
:
post a read request for runs 1 and 2
thread A: | thread B:
for r:=1 to k do | for r:=1 to k-2 do
wait until | wait until
run r is read | run r is written
sort run r | post a read for run r+2
post a write for run r |
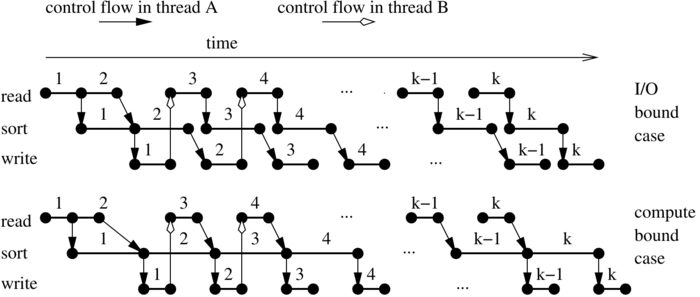
The figure above illustrates how I/O and computation is overlapped by this algorithm. Formalizing this figure, we can prove that using this approach an input of size N can be transformed into sorted runs of size 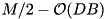 in time
in time 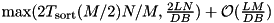 , where
, where 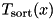 denotes the time for sorting x elements internally and where L is the time needed for a parallel I/O step.
denotes the time for sorting x elements internally and where L is the time needed for a parallel I/O step.
In [26] one can find an algorithm which generates longer runs of average length 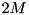 and overlaps I/O and computation.
and overlaps I/O and computation.
We want to merge k sorted sequences comprising N' elements stored in 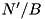 blocks (In practical situations, where a single merging phase suffices, we will have
blocks (In practical situations, where a single merging phase suffices, we will have 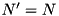 ). In each iteration, the merging thread chooses the smallest remaining element from the k sequences and hands it over to the I/O thread. Prediction of read operations is based on the observation that the merging thread does not need to access a block until its smallest element becomes the smallest unread element. We therefore record the smallest keys of each block during run formation. By merging the resulting k sequences of smallest elements, we can produce a sequence
). In each iteration, the merging thread chooses the smallest remaining element from the k sequences and hands it over to the I/O thread. Prediction of read operations is based on the observation that the merging thread does not need to access a block until its smallest element becomes the smallest unread element. We therefore record the smallest keys of each block during run formation. By merging the resulting k sequences of smallest elements, we can produce a sequence 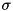 of block identifiers that indicates the exact order in which blocks are logically read by the merging thread. The overhead for producing and storing the prediction data structure is negligible because its size is a factor at least B smaller than the input.
of block identifiers that indicates the exact order in which blocks are logically read by the merging thread. The overhead for producing and storing the prediction data structure is negligible because its size is a factor at least B smaller than the input.
The prediction sequence 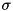 is used as follows. The merging thread maintains the invariant that it always buffers the k first blocks in
is used as follows. The merging thread maintains the invariant that it always buffers the k first blocks in 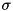 that contain unselected elements, i.e., initially, the first k blocks from
that contain unselected elements, i.e., initially, the first k blocks from 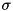 are read into these merge buffers. When the last element of a merge buffer block is selected, the now empty buffer frame is returned to the I/O thread and the next block in
are read into these merge buffers. When the last element of a merge buffer block is selected, the now empty buffer frame is returned to the I/O thread and the next block in 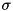 is read.
is read.
The keys of the smallest elements in each buffer block are kept in a tournament tree data structure [38] so that the currently smallest element can be selected in time 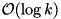 . Hence, the total internal work for merging is
. Hence, the total internal work for merging is 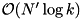 .
.
We have now defined multi-way merging from the point of view of the sorting algorithm. Our approach to merging slightly deviates from previous approaches that keep track of the run numbers of the merge blocks and pre-assign each merge block to the corresponding input sequence. In these approaches also the last key in the previous block decides about the position of a block in 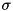 . The correctness of our approach is shown in [26]. With respect to performance, both approaches should be similar. Our approach is somewhat simpler, however — note that the merging thread does not need to know anything about the k input runs and how they are allocated. Its only input is the prediction sequence
. The correctness of our approach is shown in [26]. With respect to performance, both approaches should be similar. Our approach is somewhat simpler, however — note that the merging thread does not need to know anything about the k input runs and how they are allocated. Its only input is the prediction sequence 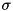 . In a sense, we are merging individual blocks and the order in
. In a sense, we are merging individual blocks and the order in  makes sure that the overall effect is that the input runs are merged. A conceptual advantage is that data within a block decides about when a block is read.
makes sure that the overall effect is that the input runs are merged. A conceptual advantage is that data within a block decides about when a block is read.
Although we can predict the order in which blocks are read, we cannot easily predict how much internal work is done between two reads. For example, consider k identical runs storing the sequence 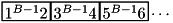 . After initializing the merge buffers, the merging thread will consume
. After initializing the merge buffers, the merging thread will consume 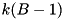 values '1' before it posts another read. Then it will post one read after selecting each of the next k values (2). Then there will be a pause of another
values '1' before it posts another read. Then it will post one read after selecting each of the next k values (2). Then there will be a pause of another 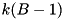 steps and another k reads are following each other quickly, etc. We explain how to overlap I/O and computation despite this irregularity using the I/O model of Aggarwal and Vitter [3] that allows access to D arbitrary blocks within one I/O step. To model overlapping of I/O and computation, we assume that an I/O step takes time L and can be done in parallel with internal computations. We maintain an overlap buffer that stores up to
steps and another k reads are following each other quickly, etc. We explain how to overlap I/O and computation despite this irregularity using the I/O model of Aggarwal and Vitter [3] that allows access to D arbitrary blocks within one I/O step. To model overlapping of I/O and computation, we assume that an I/O step takes time L and can be done in parallel with internal computations. We maintain an overlap buffer that stores up to 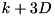 blocks in a FIFO manner (see figure above). Whenever the overlap buffer is non-empty, a read can be served from it without blocking. Writing is implemented using a write buffer FIFO with
blocks in a FIFO manner (see figure above). Whenever the overlap buffer is non-empty, a read can be served from it without blocking. Writing is implemented using a write buffer FIFO with 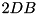 elements capacity. An I/O thread inputs or outputs D blocks in time L using the following strategy: Whenever no I/O is active and at least
elements capacity. An I/O thread inputs or outputs D blocks in time L using the following strategy: Whenever no I/O is active and at least 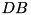 elements are present in the write buffer, an output step is started. When no I/O is active, less than D output blocks are available, and at least D overlap buffers are unused, then the next D blocks from
elements are present in the write buffer, an output step is started. When no I/O is active, less than D output blocks are available, and at least D overlap buffers are unused, then the next D blocks from 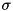 are fetched into the overlap buffer. This strategy guarantees that merging k sorted sequences with a total of N' elements can be implemented to run in time
are fetched into the overlap buffer. This strategy guarantees that merging k sorted sequences with a total of N' elements can be implemented to run in time 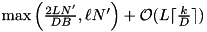 where
where 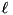 is the time needed by the merging thread to produce one element of output and L is the time needed to input or output D arbitrary blocks [26].
is the time needed by the merging thread to produce one element of output and L is the time needed to input or output D arbitrary blocks [26].
The I/Os for the run formation and for the output of merging are perfectly balanced over all disks if all sequences are striped over the disks, i.e., sequences are stored in blocks of B elements each and the blocks numbered 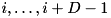 in a sequence are stored on different disks for all i. In particular, the original input and the final output of sorting can use any kind of striping.
in a sequence are stored on different disks for all i. In particular, the original input and the final output of sorting can use any kind of striping.
The merging algorithm presented above is optimal for the unrealistic model of Aggarwal and Vitter [3] which allows to access any D blocks in an I/O step. This facilitates good performance for fetching very irregularly placed input blocks. However, this model can be simulated using D independent disks using randomized striping allocation [54] and a prefetch buffer of size 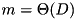 blocks: In almost every input step,
blocks: In almost every input step, 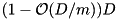 blocks from prefetch sequence
blocks from prefetch sequence 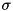 can be fetched [26].
can be fetched [26].
Run Formation. We build runs of a size close to 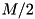 but there are some differences to the simple algorithm from Run Formation. Overlapping of I/O and computation is achieved using the call-back mechanism supported by the I/O layer. Thus, the sorter remains portable over different operating systems with different interfaces to threading.
but there are some differences to the simple algorithm from Run Formation. Overlapping of I/O and computation is achieved using the call-back mechanism supported by the I/O layer. Thus, the sorter remains portable over different operating systems with different interfaces to threading.
We have two implementations with respect to the internal work: stxxl::sort is a comparison based sorting using std::sort from STL to sort the runs internally; stxxl::ksort exploits integer keys and has smaller internal memory bandwidth requirements for large elements with small key fields. After reading elements using DMA (i.e. the STXXL direct access), we extract pairs 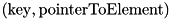 , sort these pairs, and only then move elements in sorted order to write buffers from where they are output using DMA.
, sort these pairs, and only then move elements in sorted order to write buffers from where they are output using DMA.
Furthermore, we exploit random keys. We use two passes of MSD (most significant digit) radix sort of the key-pointer pairs. The first pass uses the m most significant bits where m is a tuning parameter depending on the size of the processor caches and of the TLB (translation look-aside buffer). This pass consists of a counting phase that determines bucket sizes and a distribution phase that moves pairs. The counting phase is fused into a single loop with pair extraction. The second pass of radix sort uses a number of bits that brings us closest to an expected bucket size of two. This two-pass algorithm is much more cache efficient than a one-pass radix sort. (On our system we get a factor of 3.8 speedup over the one pass radix sort and a factor of 1.6 over STL's sort which in turn is faster than a hand tuned quicksort (for sorting 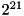 pairs storing a random four byte key and a pointer). The remaining buckets are sorted using a comparison based algorithm: Optimal straight line code for
pairs storing a random four byte key and a pointer). The remaining buckets are sorted using a comparison based algorithm: Optimal straight line code for 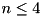 , insertion sort for
, insertion sort for 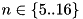 , and quicksort for
, and quicksort for  .
.
Multi-way Merging. We have adapted the tuned multi-way merger from [50], i.e. a tournament tree stores pointers to the current elements of each merge buffer.
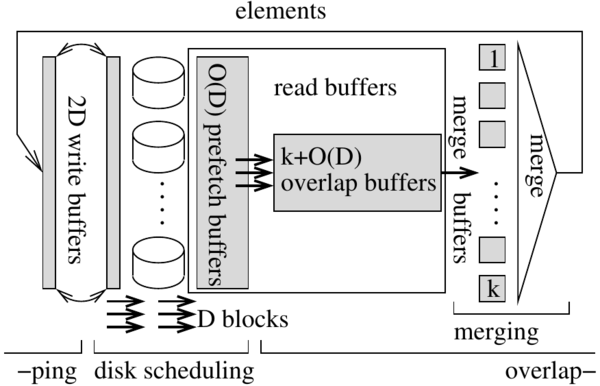
Overlapping I/O and Computation. We integrate the prefetch buffer and the overlap buffer to a read buffer. We distribute the buffer space between the two purposes of minimizing disk idle time and overlapping I/O and computation indirectly by computing an optimal prefetch sequence for a smaller buffer space.
Asynchronous I/O. I/O is performed without any synchronization between the disks. The prefetcher computes a sequence 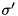 of blocks indicating the order in which blocks should be fetched. As soon as a buffer block becomes available for prefetching, it is used to generate an asynchronous read request for the next block in
of blocks indicating the order in which blocks should be fetched. As soon as a buffer block becomes available for prefetching, it is used to generate an asynchronous read request for the next block in 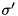 . The I/O layer of STXXL queues this request at the disk storing the block to be fetched. The thread for this disk serves the queued request in FIFO manner. All I/O is implemented without superfluous copying. STXXL opens files with the option
. The I/O layer of STXXL queues this request at the disk storing the block to be fetched. The thread for this disk serves the queued request in FIFO manner. All I/O is implemented without superfluous copying. STXXL opens files with the option O_DIRECT so that blocks are directly moved by DMA (direct memory access) to user memory. A fetched block then travels to the prefetch/overlap buffer and from there to a merge buffer simply by passing a pointer. Similarly, when an element is merged, it is directly moved from the merge buffer to the write buffer and a block of the write buffer is passed to the output queue of a disk simply by passing a pointer to the the I/O layer of STXXL that then uses write to output the data using DMA.